
Figure 1 - The airfoil moment and lift forces
On a sailboat, the combined center of effort of the sail should be 5% of the water line length behind the center of lateral resistance. Sound familiar? The center of effort (CE) refers to the sails, and the center of lateral resistance (CLR) is basically the center of rotation when a sailboat gets pushed from the side.
When a wind hits a sailboat from the side, the effect of the wind can be viewed as a single force located at the CE. Likewise, the effect the wind has on the boat itself can be viewed as a single force at the CLR. By locating the CE behind the CLR, the boat will naturally turn its bow (the front of the boat) into the wind, which will reduce the sail area facing the wind and reduce the force generated by the wind on the sails.
Hopefully it is obvious that the relative locations of the CE and CLR, are based on very similar concepts used to locate the CG on a sailplane. This illustrates the similarities between sailboat and sailplane design. There are of course several other including the design of the sail, and the reduction of drag of the boat against the water.
Unfortunately, while these concepts may have provided a good foundation for early aerodynamics, they do not provide a complete understanding, Unfortunately today, we still hear the term center of pressure used with respect to airfoils. In the 3rd edition of Aerodynamics for Model Airplanes, Martin Simmons shows two polar diagrams for the Clark-Y airfoil. The first, from 1924, shows a center of pressure measurement. The second, from 1931, shows separate lift and moment measurements. In other words, use of center of pressure was already becoming obsolete in 1931, over three quarters of a century ago.
While it is easy to understand why early aerodynamicists, used the center of pressure concept, you would think that it would rarely be mentioned today. This note discusses the two forces created by cambered airfoils, and the difficulties caused when only a single force, center of pressure, is considered. Martin Simmons discussed these concepts in an RCSD article on .... 1994 entitiled "....". This article provides simple review, and a plot showing how center-of-pressure and moment coefficient are related.
A moment describes a rotational force, or torque.
A wrench is used to produce a moment to twist a bolt.
The distance between the force and the center of rotation
is the moment-arm.
The magnitude or size of the moment
is the force times the length of the moment-arm.
A longer wrench can produce the same torque with a smaller force.
M = F * d
where
M is the moment,
F is the force, and
d is the moment arm.
The use of a wrench also produces a translational force, F, as well as a moment. The translational force pushes the bolt and assembly it is attached too in the direction of the force. The assembly will move in that direction if it is not heavy enough or held down.
A motor is an example of a device that only produces a moment. Once it is in motion, it will remain stationary. When it is started, the entire motor assembly will be forced to rotate in the opposite direction as its shaft until the rotational speed stabilizes.
A cambered, or non-symetrical airfoil produces both a translational force or lift, and a moment. The aerodynamic center (AC) of the airfoil defines the center of rotation of the moment, as well as, the center of lift. Using the aerodynamic center as the reference point, the moment and translational forces produced by an airfoil can be viewed independently. See figure-1.

With this in mind, it becomes clear that an airfoil producing zero lift can still produce a moment, and is true even when the AOA causes a negative lifting force as required in inverted flight. Because the moment and lift are independent forces it is hopefully clear that the center of lift can remain stationary.
A simple example may be a small sheet of cardboard that is partially bent in half such that it is angled. When dropped, it will spin around the axis of the bend. Consider a flat plate used as an airfoil with flaps. When the flaps are in line with the flat plate, the moment should be zero. At a constant airspeed, the moment will increase as the flaps are deflected.
The center-of-pressure concept assumes that an airfoil
produces a single force, lift,
and that the lift causes the moment.
Since the measured moment of many airfoils is constant,
this concept implies that the moment-arm must increase,
that the lift moves rearward,
as the angle of attack (AOA) and the lift decrease.
d = M / L
where lift, L, replaces force, F.
This implies that as the AOA is decreased toward the point of zero lift, a point is reached where the lift is actually behind the trailing edge, and ultimately goes to infinity as the lift becomes zero. (What happens when lift becomes negative, as in inverted flight? Does is move ahead of the leading edge?)
The center-of-pressure curves on the older airfoil plots
indicate a most forward chord position at maximum lift,
and more rearward chord position as the lift decreases.
There is little change in chord position
as the lift is reduced near its maximum.
But it reaches a point
where the chord position changes very quickly
as the lift decreases.
CP = AC + CM / CL
where
CP is the center-of-pressure or chord position, and
AC is the aerodynamic center.
Figure-2 reproduces the center-of-pressure plots using the equation above, for three moment coefficients, and an aerodynamic center at the 1/4 chord position. It compares well to the old airfoil plots.
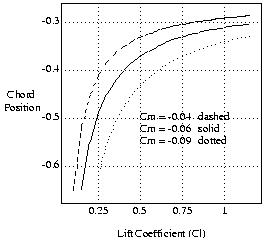
This curve shows me that the two airfoil plots, one with center-of-pressure and the other with Cm, provide the same information. It convinces me that the center-of-pressure concept is obsolete. I can understand why wind tunnel measurements were originally made using center-of-pressure, and as tunderstanding improved, were changed to provide moment coefficient. I hope i never read another article describing airfoils using the center-of-pressure.