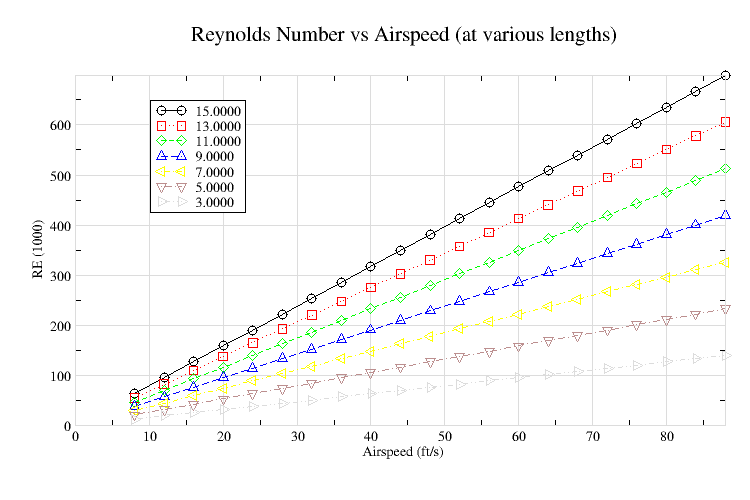
Figure 1
Because of my limited experience, I don't have a feel for the Reynolds Number (RE) that the various wings sections are operating at without going through the calculations which I then second guess. I find the two plots below helpful in quickly giving me the numbers I need.
RE is calculated from the following equation, where v is airspeed in m/s, l is length in m, rho is air density (1.225 kg/m3), and viscosity of air (0.00001789 N-s/m2).
RE = v * l * rho / viscosity
Airspeed and length in english units of feet can easily be converted to meters in order to use the above equation, avoiding the need to find the english equivalents of rho and viscosity. The constant, rho / viscosity, is equal to 68474, and the english equivalent is 6352. For example, (from Anderson's Introduction to Flight) the RE for an airspeed of 120 m/s and a lenght of 0.05 is 410844. However, such calculations can be avoided by using Figure-1. It provides a set of curves, for various chord lengths, relating airspeed to Reynolds Number.

Determining the airspeed range for a particular aircraft can also be tedious. It can be determined using the following equation where W is weight, S is wing area, and Cl is the lift coefficient.
v = sqrt (W / (0.5 * rho * S * Cl))
The range of values can be simplified by recognizing that W/S is simply wing-loading, which has a practical range. Cl is also limited, maximum speed near 0.1, minimum speed and sink near 0.9, and best lift/drag (L/D) is probably around 0.7. Figure-2 provides the airspeeds over a range of Cl values as the wing-loading varies.
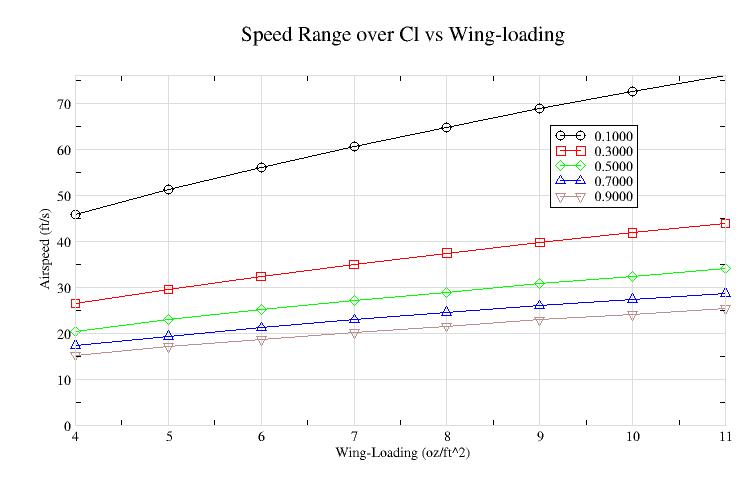
For example, the airspeed range for a wing-loading of 8 oz/sq.ft. is 22 to 65 ft/sec, and best L/D around 25. Figure-1 can then be used to consider the range of Reynolds Numbers over this speed range for the wing chords of the planform being considered. A planform with a root chord of 9" and tip chord of 5", will have RE ranges from 100k to 300k at the root, and 50K to 150K at the tip. And airfoil performance can be better evaluated knowing the Reynolds Numbers that they will be operating at.